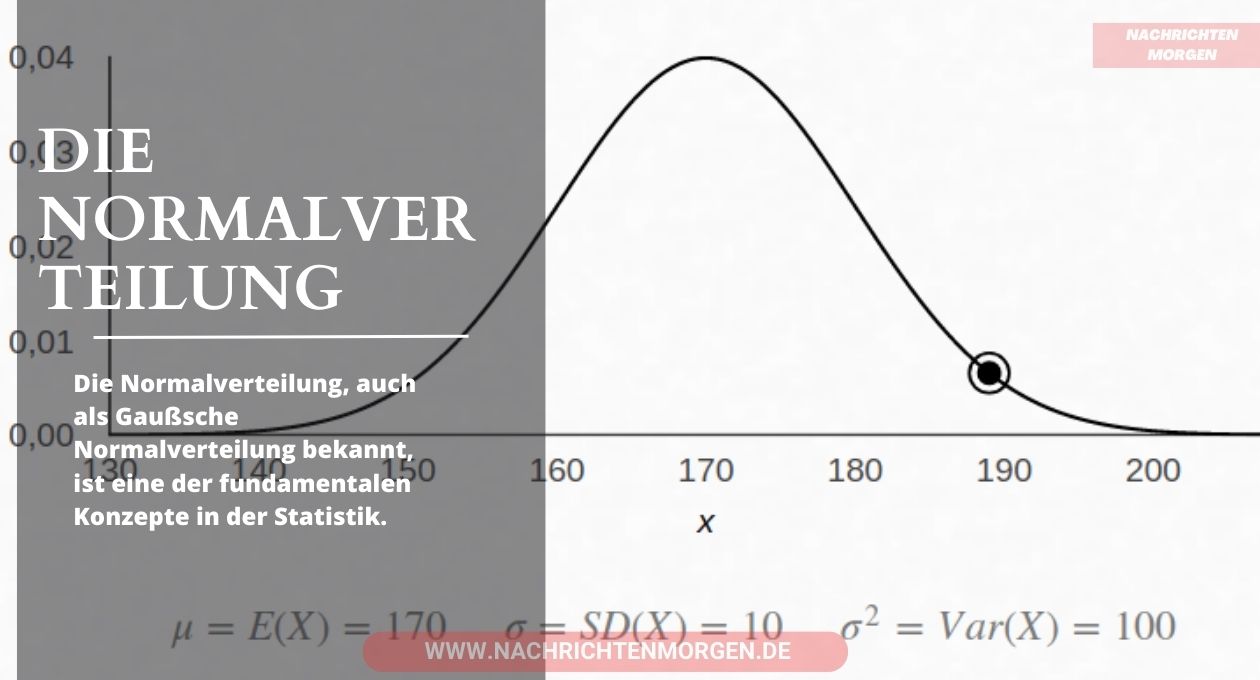
Die Normalverteilung, auch als Gaußsche Normalverteilung bekannt, ist eine der fundamentalen Konzepte in der Statistik. Sie bildet die Basis vieler statistischer Analysen und Modelle. In diesem Blog werden wir die verschiedenen Aspekte der Normalverteilung beleuchten, von ihrer Definition bis hin zu Anwendungen und Tests auf Normalverteilung.
Definition der Normalverteilung
Die Normalverteilung, auch Gaußsche Verteilung genannt, ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die durch ihren Mittelwert und ihre Standardabweichung definiert wird. Sie wird oft als Glockenkurve dargestellt, da ihre graphische Darstellung einem Glockenprofil ähnelt.
Merkmale der Normalverteilung
Ein charakteristisches Merkmal der Normalverteilung ist, dass sie symmetrisch um ihren Mittelwert verläuft. Das bedeutet, dass die Datenwerte um den Mittelwert herum verteilt sind, wobei die meisten Werte nahe dem Mittelwert liegen und die restlichen Werte gleichmäßig auf beiden Seiten des Mittelwerts abnehmen.
Die Standardnormalverteilung
Die Standardnormalverteilung ist eine besondere Form der Normalverteilung, bei der der Mittelwert 0 und die Standardabweichung 1 beträgt. Sie dient als Referenzverteilung für die Umwandlung von Werten einer beliebigen Normalverteilung in Standardwerte.
Viertel Unze Gold? Ceyrek Altin Kac Euro
Anwendung der Normalverteilung
Die Normalverteilung findet in vielen Bereichen Anwendung. Sie wird in der Wirtschaft, in der Psychologie, in den Naturwissenschaften und in vielen anderen Bereichen, in denen statistische Analysen durchgeführt werden, verwendet.
Tests auf Normalverteilung
Es gibt verschiedene statistische Tests, mit denen überprüft werden kann, ob eine Datenverteilung normal ist. Beispiele dafür sind der Kolmogorov-Smirnov-Test, der Lilliefors-Test und der Anderson-Darling-Test.
Die Zentraler Grenzwertsatz
Der zentrale Grenzwertsatz ist ein grundlegendes Konzept in der Statistik, das besagt, dass die Summe einer großen Anzahl von unabhängigen und identisch verteilten Zufallsvariablen näherungsweise normal verteilt ist. Dies ist einer der Gründe, warum die Normalverteilung in der Praxis so häufig auftritt.
Die 68-95-99.7 Regel
Die 68-95-99.7 Regel ist eine praktische Regel zur Beschreibung der Normalverteilung. Sie besagt, dass etwa 68% der Werte innerhalb einer Standardabweichung des Mittelwerts liegen, 95% innerhalb von zwei Standardabweichungen und 99.7% innerhalb von drei Standardabweichungen.
Schlussfolgerung
Die Normalverteilung ist ein mächtiges Werkzeug in der Statistik. Sie bietet eine einfache und effektive Methode zur Modellierung und Analyse von Daten und hilft dabei, komplexe Phänomene zu verstehen und Vorhersagen zu treffen.
Was ist eine Normalverteilung?
Die Normalverteilung ist eine Art von Wahrscheinlichkeitsverteilung, bei der die Werte um einen zentralen Mittelwert herum symmetrisch angeordnet sind. Die charakteristische Glockenkurve zeigt, dass die meisten Datenpunkte nahe dem Mittelwert liegen und die Verteilung symmetrisch um diesen Mittelwert herum verläuft.
In der Statistik ist die Normalverteilung von zentraler Bedeutung. Sie wird oft verwendet, um natürliche Phänomene zu modellieren, da viele natürliche Merkmale normalverteilt sind. Beispielsweise sind Körpergröße und Intelligenzquotient normalverteilt — die meisten Menschen haben eine durchschnittliche Größe oder einen durchschnittlichen IQ, während nur wenige extrem groß, klein, hochintelligent oder weniger intelligent sind.
Punkte in Noten Umrechnen
Die Normalverteilung wird durch zwei Parameter bestimmt: den Erwartungswert (Mittelwert) und die Standardabweichung. Der Erwartungswert gibt den Durchschnitt oder das Zentrum der Verteilung an. Die Standardabweichung misst die Streuung oder Variation in der Verteilung. Eine geringe Standardabweichung bedeutet, dass die Werte nahe am Mittelwert liegen, während eine hohe Standardabweichung bedeutet, dass die Werte über einen größeren Bereich verteilt sind.
Ein weiterer Aspekt der Normalverteilung ist die Tatsache, dass etwa 68% aller Werte innerhalb einer Standardabweichung vom Mittelwert entfernt liegen, etwa 95% innerhalb von zwei Standardabweichungen und etwa 99,7% innerhalb von drei Standardabweichungen. Dies wird als die 68-95-99,7-Regel oder die Dreisigma-Regel bezeichnet.
Die Normalverteilung ist auch bekannt als Gaußsche Verteilung, benannt nach dem berühmten deutschen Mathematiker Carl Friedrich Gauss. Gauss trug maßgeblich zur Entwicklung der Theorie der Normalverteilung bei. Er führte das Konzept der Normalverteilung in seine Arbeiten zur Wahrscheinlichkeitsrechnung und Statistik ein, was einen Paradigmenwechsel in diesen Bereichen bewirkte.
Die Normalverteilung hat viele interessante Eigenschaften und Anwendungen. Sie wird in verschiedenen Zweigen der Wissenschaft, Technologie, Wirtschaft und anderen Bereichen eingesetzt. Eine ihrer bemerkenswertesten Anwendungen ist die Inferenzstatistik, bei der die Normalverteilung zur Durchführung von Hypothesentests und zur Erstellung von Konfidenzintervallen verwendet wird.
Trotz ihrer weit verbreiteten Anwendung ist die Normalverteilung nicht immer die beste oder geeignetste Verteilung für jede Situation. In einigen Fällen können die Daten stark schief sein oder extreme Werte aufweisen, die nicht gut durch eine Normalverteilung modelliert werden. In solchen Fällen können andere Verteilungen, wie die logistische Verteilung oder die t-Verteilung, geeigneter sein.
Es ist wichtig zu beachten, dass die Normalverteilung ein ideales Modell ist, das auf die Realität angewendet wird. Es ist unwahrscheinlich, dass echte Datensätze perfekt normalverteilt sind, aber viele sind nah genug, um die Normalverteilung als gutes Modell zu verwenden.
Schließlich spielt die Normalverteilung auch eine Schlüsselrolle in der modernen Datenanalyse und maschinellem Lernen. Sie hilft bei der Modellierung von Unsicherheiten und macht Vorhersagen möglich, indem sie Wahrscheinlichkeitsverteilungen über mögliche Ergebnisse liefert.
Die Gaußsche Normalverteilung und ihre Eigenschaften
Die gaußsche Normalverteilung, benannt nach dem Mathematiker Carl Friedrich Gauß, ist ein Synonym für die Normalverteilung. Sie wird durch zwei Parameter definiert: den Mittelwert (Erwartungswert) und die Standardabweichung. Der Mittelwert bestimmt den zentralen Punkt der Verteilung, während die Standardabweichung die Streuung der Daten um den Mittelwert angibt.
Eidesstattliche Erklärung: Definition, Bedeutung
Die Dichtefunktion und die Verteilungsfunktion der Normalverteilung
Die Dichtefunktion beschreibt die Wahrscheinlichkeit, dass eine Variable einen bestimmten Wert annimmt. Für die Normalverteilung ist die Dichtefunktion die berühmte Glockenkurve. Die Verteilungsfunktion gibt die Wahrscheinlichkeit an, dass eine Zufallsvariable einen Wert kleiner oder gleich einem bestimmten Wert annimmt.
Anwendungen und Beispiele der Normalverteilung
Die Normalverteilung findet in vielen Bereichen Anwendung, wie z.B. in der Finanzanalyse, der Medizin, der Psychologie und der Qualitätssicherung. Ein klassisches Beispiel ist der IQ-Test. Die IQ-Werte sind oft normalverteilt, was es ermöglicht, Intelligenz auf standardisierte Weise zu bewerten.
Tests auf Normalverteilung
Um festzustellen, ob Daten normalverteilt sind, können statistische Tests wie der Kolmogorov-Smirnov-Test oder der Shapiro-Wilk-Test verwendet werden. Diese Tests überprüfen, ob die Daten signifikant von einer Normalverteilung abweichen.
Multivariate Normalverteilung
Die multivariate Normalverteilung erweitert das Konzept der Normalverteilung auf mehrere korrelierte Variablen und bildet ihre gemeinsame Verteilung ab. Sie wird durch einen Vektor von Mittelwerten und einer Kovarianzmatrix definiert. Der Mittelwertvektor gibt den erwart
Normalverteilung in Excel und SPSS
Sowohl in Excel als auch in SPSS können Sie die Normalverteilung für Ihre Daten analysieren. In Excel können Sie die Funktionen wie “NORM.DIST” und “NORM.INV” verwenden, um Wahrscheinlichkeiten und kritische Werte zu berechnen. In SPSS können Sie Tests auf Normalverteilung durchführen, um die Annahme der Normalverteilung zu überprüfen.
Erwartungsert Normalverteilung
Der Erwartungswert einer Normalverteilung ist ein grundlegendes Konzept in der Statistik und Wahrscheinlichkeitstheorie. Er gibt den durchschnittlichen Wert einer Zufallsvariablen an, wenn ein Experiment unendlich oft wiederholt wird.
Die Normalverteilung, auch als Gaußsche Verteilung bekannt, ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die durch ihren Erwartungswert (Mittelwert) und die Standardabweichung definiert ist. Die Normalverteilung ist symmetrisch und ihre Dichtefunktion bildet eine Glockenkurve.
Erstellen Sie Beeindruckende Schriftgenerator
Der Erwartungswert der Normalverteilung entspricht ihrem Mittelwert. Dies bedeutet, dass bei einer ideal normalverteilten Population der Durchschnitt der gesammelten Daten der erwartete Wert ist.
Die Formel für den Erwartungswert μ einer Normalverteilung ist einfach μ selbst. Dies ist so, weil die Normalverteilung eine symmetrische Verteilung ist, und deshalb ist der Mittelwert gleich dem Modus und dem Median der Verteilung.
In der Praxis kann der Erwartungswert der Normalverteilung verwendet werden, um Vorhersagen zu treffen. Zum Beispiel, wenn eine Studentenpopulation normalverteilt ist in Bezug auf ihre Testergebnisse, dann kann man vorhersagen, dass die meisten Schüler nahe dem Durchschnitt liegen werden.
Es ist wichtig zu beachten, dass der Erwartungswert keine zwingende Realität ist, sondern eine statistische Wahrscheinlichkeit. Es ist durchaus möglich, dass bei einer einzelnen Messung ein Wert weit vom Erwartungswert entfernt ist.
Die Bestimmung des Erwartungswertes einer Normalverteilung ist ein mächtiges Werkzeug in vielen Bereichen, einschließlich der Wissenschaft, Technik, Wirtschaft, Sozialwissenschaften und vielen anderen.
Auch wenn der Erwartungswert ein einfacher Durchschnitt ist, liefert er wertvolle Einsichten in die zugrundeliegende Verteilung und ermöglicht es uns, fundierte Vorhersagen und Entscheidungen zu treffen.
Verteilungsfunktion Normalverteilung
Die Normalverteilung, auch als Gaußsche Verteilung bekannt, ist eine der am häufigsten verwendeten Verteilungen in der Statistik. Sie zeichnet sich durch ihre charakteristische Glockenform aus und wird oft verwendet, um naturwissenschaftliche und soziale Phänomene zu modellieren, bei denen die Beobachtungen um einen Mittelwert streuen.
Die Wahrscheinlichkeitsdichtefunktion der Normalverteilung ist symmetrisch und ihr Maximum liegt am Erwartungswert. Die Form der Verteilung wird durch den Erwartungswert und die Standardabweichung bestimmt. Der Erwartungswert gibt den Mittelwert der Verteilung an, während die Standardabweichung ein Maß für die Streuung der Daten um den Mittelwert ist.
Die Normalverteilung wird durch die Gaußsche Glockenkurve repräsentiert. Die Fläche unter der Glockenkurve entspricht der Wahrscheinlichkeit, dass eine zufällige Variable aus einer normalverteilten Population einen bestimmten Wert annimmt. Die gesamte Fläche unter der Kurve ist 1, was bedeutet, dass die Summe aller Wahrscheinlichkeiten 1 ist.
Einführung in Die Plattform IServ Obs
Die Normalverteilung hat einige wichtige Eigenschaften. Erstens, etwa 68% der Daten liegen innerhalb einer Standardabweichung vom Mittelwert entfernt, etwa 95% liegen innerhalb von zwei Standardabweichungen und etwa 99,7% liegen innerhalb von drei Standardabweichungen. Dies wird oft als die “68-95-99,7 Regel” bezeichnet.
Zweitens ist die Normalverteilung unimodal, was bedeutet, dass sie nur einen einzigen, deutlichen “Höhepunkt” oder Modus hat. Dieser Modus fällt auch mit dem Median und dem Mittelwert zusammen, was bei anderen Verteilungen nicht immer der Fall ist.
Drittens, die Normalverteilung ist kontinuierlich, d.h., sie nimmt jeden Wert innerhalb eines bestimmten Bereichs an. Dies unterscheidet sie von diskreten Verteilungen, die nur bestimmte, getrennte Werte annehmen können.
Viertens, eine Besonderheit der Normalverteilung ist die zentrale Grenzwertsatz. Dieser Satz besagt, dass die Summe einer großen Anzahl von unabhängigen und identisch verteilten Zufallsvariablen sich einer Normalverteilung annähert, unabhängig von der Form der ursprünglichen Verteilung.
Schließlich ist es erwähnenswert, dass trotz ihrer weit verbreiteten Verwendung, die Normalverteilung nicht immer die beste Wahl zur Modellierung realer Daten ist. Es gibt viele Situationen, in denen die Annahme der Normalverteilung nicht gerechtfertigt ist und andere Verteilungen besser geeignet sind.
Normalverteilung Wahrscheinlichkeit Berechnen
Die Normalverteilung, auch bekannt als Gaußsche Verteilung, ist eine der häufigsten Wahrscheinlichkeitsverteilungen in der Statistik. Sie ist besonders wichtig aufgrund des zentralen Grenzwertsatzes, der besagt, dass die Summe vieler unabhängiger und identisch verteilter Zufallsvariablen ungefähr normalverteilt ist.
Die Wahrscheinlichkeit in einer normalverteilten Zufallsvariable kann mithilfe der Normalverteilungsfunktion berechnet werden. Diese Funktion wird durch ihre beiden Parameter, den Erwartungswert (Mittelpunkt der Verteilung) und die Standardabweichung (Maß für die Streuung der Werte), bestimmt.
Eine umfassende Liste von Ideen und Antworten Land mit
Die Berechnung der Wahrscheinlichkeit für einen bestimmten Wertbereich geschieht durch Integration der Normalverteilungsfunktion über diesen Bereich. Beispielsweise kann die Wahrscheinlichkeit, einen Wert zwischen -1 und +1 in einer Standardnormalverteilung (Erwartungswert 0, Standardabweichung 1) zu finden, berechnet werden, indem die Normalverteilungsfunktion von -1 bis +1 integriert wird.
Es ist zu beachten, dass in der Praxis die direkte Integration der Normalverteilungsfunktion oft durch Standardtabellen oder numerische Verfahren ersetzt wird. Diese Tabellen oder Verfahren geben die kumulierte Wahrscheinlichkeit für einen gegebenen Wertbereich in einer Standardnormalverteilung an.
Die Berechnung der Wahrscheinlichkeit eines Bereichs, der nicht um den Erwartungswert zentriert ist, erfolgt durch Umwandlung in eine standardisierte Normalverteilung. Dies geschieht durch Subtraktion des Erwartungswertes von den Grenzen des Bereichs und Division durch die Standardabweichung.
Nach der Standardisierung kann die Wahrscheinlichkeit des Bereichs durch Integration der Standardnormalverteilungsfunktion oder Verwendung von Standardtabellen oder numerischen Verfahren berechnet werden. Die resultierende Wahrscheinlichkeit ist die gleiche wie in der ursprünglichen Normalverteilung.
Die Berechnung der Wahrscheinlichkeit in der Normalverteilung ist ein grundlegendes Werkzeug in vielen Bereichen der Statistik, einschließlich der Hypothesentestung und der Schätzung von Konfidenzintervallen. Sie ist ein unverzichtbares Element in der Toolbox jedes Statistikers.
Zusammenfassend lässt sich sagen, dass die Normalverteilung eine Schlüsselrolle in der Statistik spielt. Durch das Verständnis, wie man Wahrscheinlichkeiten in einer Normalverteilung berechnet, kann man ein tieferes Verständnis für statistische Konzepte und Methoden gewinnen.
Binomialverteilung Normalverteilung
Die Binomialverteilung ist eine der grundlegenden Wahrscheinlichkeitsverteilungen in der Statistik. Sie beschreibt die Anzahl der Erfolge in einer bestimmten Anzahl von unabhängigen Versuchen. Jeder Versuch hat nur zwei mögliche Ausgänge – Erfolg oder Misserfolg. Ein typisches Beispiel für eine Binomialverteilung ist der Wurf einer Münze.
Die Normalverteilung ist ebenfalls eine zentrale Wahrscheinlichkeitsverteilung in der Statistik. Sie wird oft als Glockenkurve dargestellt und beschreibt in vielen natürlichen und sozialwissenschaftlichen Phänomenen verteilte Daten. Beispielsweise gelten Größe und Intelligenz in menschlichen Populationen häufig als normalverteilt.
Wie Man Sich Richtig Entschuldigung Für Die Schule
Der Zusammenhang zwischen Binomial- und Normalverteilung ist faszinierend. Während die Binomialverteilung die Wahrscheinlichkeitsverteilung von diskreten Ereignissen ist, ist die Normalverteilung eine kontinuierliche Verteilung. Aber unter bestimmten Bedingungen kann die Binomialverteilung durch die Normalverteilung approximiert werden.
Dieser Approximationsprozess wird als Zentraler Grenzwertsatz bezeichnet. Er besagt, dass wenn die Anzahl der Versuche in einer binomialverteilten Zufallsvariablen gegen unendlich geht, die Form der Verteilung einer Normalverteilung immer ähnlicher wird.
Diese Approximation ist besonders nützlich in der statistischen Analyse, da die Normalverteilung einfacher und effizienter zu handhaben ist als die Binomialverteilung. Insbesondere ermöglicht die Normalverteilung die Anwendung zahlreicher statistischer Tests und Verfahren.
In der Praxis bedeutet dies, dass wir oft die Normalverteilung verwenden, um reale Phänomene zu modellieren, selbst wenn die zugrunde liegenden Daten diskret sind. Dies ist insbesondere dann der Fall, wenn die Anzahl der Beobachtungen groß ist, da die Normalverteilung dann eine gute Näherung liefert.
Es ist aber wichtig zu beachten, dass die Normalverteilung nicht immer eine perfekte Lösung ist. Es gibt Situationen, in denen die Annahme einer Normalverteilung zu fehlerhaften Schlussfolgerungen führen kann, insbesondere wenn die Daten stark asymmetrisch oder in anderer Weise von der Glockenkurve abweichend sind.
Zusammenfassend lässt sich sagen, dass sowohl die Binomial- als auch die Normalverteilung wichtige Werkzeuge in der Statistik sind. Sie ermöglichen es uns, komplexe Phänomene zu analysieren und zu verstehen, und sie bieten einen Rahmen für die Durchführung von Hypothesentests und anderen statistischen Verfahren.
Normalverteilung Erwartungswert
Der Erwartungswert einer normalverteilten Zufallsvariablen ist der Wert, der im Durchschnitt zu erwarten ist, wenn das Experiment unendlich oft durchgeführt wird. Er wird auch als das “Mittel” oder der “Durchschnittswert” der Normalverteilung bezeichnet.
Warum Darf Man Sterbende Nicht Beim Namen Rufen?
Für eine Normalverteilung liegt der Erwartungswert immer in der Mitte der Verteilung. Dies bedeutet, dass die Wahrscheinlichkeit, einen Wert unter dem Erwartungswert zu ziehen, genau gleich der Wahrscheinlichkeit ist, einen Wert über dem Erwartungswert zu ziehen. Es handelt sich also um eine symmetrische Verteilung.
Der Erwartungswert einer Normalverteilung wird durch den Parameter μ (Mü) dargestellt, der oft als “Standortparameter” bezeichnet wird. Dies liegt daran, dass der Erwartungswert den “Standort” oder das Zentrum der Normalverteilung auf einer Zahlengeraden festlegt.
Die Normalverteilung ist eine der am häufigsten vorkommenden Verteilungen in der Statistik und wird oft verwendet, um reale Phänomene darzustellen. Dazu gehören zum Beispiel die Größe von Menschen, die Performance von Aktien und viele andere Messungen, die in der Natur vorkommen.
Es ist zu beachten, dass der Erwartungswert einer Normalverteilung nicht immer ein realistischer “typischer” Wert ist. Dies liegt daran, dass der Erwartungswert durch extrem hohe oder extrem niedrige Werte beeinflusst werden kann. In diesen Fällen kann der Median (der Wert, der die Datenmenge in zwei Hälften teilt) eine bessere Darstellung des “typischen” Werts sein.
Es ist auch wichtig, zu beachten, dass der Erwartungswert nicht die einzige Kennzahl einer Normalverteilung ist. Auch die Standardabweichung, die die Streuung der Werte um den Erwartungswert misst, ist eine wichtige Kennzahl.
Zusammengefasst ist der Erwartungswert einer Normalverteilung ein wichtiger Parameter, der das Zentrum der Verteilung darstellt. Er bietet einen Durchschnittswert, aber es ist wichtig, auch die Streuung der Werte zu berücksichtigen.
Spss Normalverteilung Prüfen
Die Überprüfung der Normalverteilung in SPSS ist ein wichtiger Schritt bei vielen statistischen Analysen. Die Normalverteilung ist eine grundlegende Annahme in vielen statistischen Tests und Modellen. Um zu überprüfen, ob Ihre Daten normal verteilt sind, können Sie verschiedene Tests in SPSS verwenden.
Der Shapiro-Wilk-Test ist einer der Tests, die Sie verwenden können, um die Normalverteilung Ihrer Daten zu überprüfen. Dieser Test vergleicht die Verteilung Ihrer Daten mit der einer Normalverteilung. Der Nullhypothese dieses Tests zufolge sind die Daten normal verteilt. Wenn der p-Wert des Tests kleiner als 0,05 ist, wird die Nullhypothese abgelehnt und angenommen, dass die Daten nicht normal verteilt sind.
Glückwünsche Zum 60. Geburtstag: Eine Sammlung Von Grüßen
Ein weiterer Test, den Sie verwenden können, ist der Kolmogorov-Smirnov-Test. Dieser Test überprüft ebenfalls, ob die Daten normal verteilt sind. Jedoch ist dieser Test im Vergleich zum Shapiro-Wilk-Test weniger genau, vor allem bei kleineren Stichproben.
Sie können auch grafische Methoden zur Überprüfung der Normalverteilung in SPSS verwenden. Ein Histogramm oder ein Q-Q-Plot (Quantile-Quantile-Plot) kann dabei helfen, die Form der Verteilung Ihrer Daten zu visualisieren.
Ein Histogramm zeigt die Frequenz der Datenpunkte in verschiedenen Bereichen oder “Bins”. Wenn Ihre Daten normal verteilt sind, sollte das Histogramm die Form einer Glockenkurve haben.
Ein Q-Q-Plot vergleicht die Quantile Ihrer Daten mit den Quantilen einer Normalverteilung. Wenn Ihre Daten normal verteilt sind, sollten die Punkte in der Nähe einer geraden Linie liegen.
Es ist wichtig zu beachten, dass kein Test oder Diagramm definitiv beweisen kann, dass Ihre Daten normal verteilt sind. Stattdessen können diese Methoden nur Anhaltspunkte liefern, ob die Normalverteilungsannahme gerechtfertigt ist oder nicht.
Abschließend ist zu sagen, dass die Überprüfung der Normalverteilung ein wichtiger Schritt in vielen statistischen Analysen ist und SPSS eine Reihe von Werkzeugen bietet, um diesen Prozess zu unterstützen.
Was Ist Eine Normalverteilung
Eine Normalverteilung, auch bekannt als Gauß’sche Verteilung, ist eine der am häufigsten verwendeten Verteilungen in der Statistik. Sie ist benannt nach dem deutschen Mathematiker Carl Friedrich Gauss.
Die Normalverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die durch ihre Glockenkurve oder “Normal-Kurve” gekennzeichnet ist. Der höchste Punkt in der Kurve, oder der Modus, entspricht dem Durchschnitt (oder dem Median) der Verteilung.
Die Normalverteilung hat zwei Parameter: den Mittelwert µ und die Standardabweichung σ. Der Mittelwert gibt den Durchschnittswert der Verteilung an, während die Standardabweichung die Ausbreitung oder Varianz der Verteilung beschreibt.
Werte nahe dem Mittelwert haben die höchste Wahrscheinlichkeit, während Werte weiter entfernt vom Mittelwert eine geringere Wahrscheinlichkeit haben. Dies spiegelt sich in der Form der Glockenkurve wider.
Stundenplan: Eine praktische Anleitung zum Erstellen und Verwalten
Eine der wichtigsten Eigenschaften der Normalverteilung ist die Regel 68-95-99.7. Diese Regel besagt, dass etwa 68% der Daten innerhalb einer Standardabweichung vom Mittelwert liegen, 95% innerhalb von zwei Standardabweichungen und 99.7% innerhalb von drei Standardabweichungen.
Die Normalverteilung wird oft verwendet, um natürliche Phänomene zu beschreiben, die um einen Durchschnitt verteilt sind. Beispiele dafür sind die Körpergröße, der IQ oder die Blutdruckwerte einer Bevölkerung.
Es ist wichtig zu beachten, dass nicht alle Daten normalverteilt sind. Einige Verteilungen können eine Schiefe oder Kurtosis aufweisen, die von der Normalverteilung abweicht. In solchen Fällen können andere statistische Techniken erforderlich sein.
Trotz ihrer Einschränkungen ist die Normalverteilung ein leistungsstarkes Werkzeug in der Statistik und bietet einen wertvollen Ausgangspunkt für die Analyse von Daten.
Gaußsche Normalverteilung Iq
Die Gaußsche Normalverteilung, auch bekannt als Glockenkurve, ist eine statistische Funktion, die die Eigenschaften einer natürlichen Population beschreibt. Sie ist in vielen Bereichen der Wissenschaft und der Sozialwissenschaften von entscheidender Bedeutung, einschließlich der Messung der Intelligenz.
Der Intelligenzquotient (IQ) wird oft mit Hilfe der Gaußschen Normalverteilung gemessen. In einer gegebenen Population liegt der durchschnittliche IQ bei 100. Etwa 68% der Menschen haben einen IQ zwischen 85 und 115, während etwa 95% der Menschen einen IQ zwischen 70 und 130 haben.
Jenseits dieser Bereiche beginnen die Extremwerte. Nur 2,5% der Population haben einen IQ über 130, was als hochbegabt gilt. Ebenso haben nur 2,5% der Bevölkerung einen IQ unter 70, was als geistige Behinderung betrachtet wird.
Die Gaußsche Normalverteilung ist symmetrisch. Dies bedeutet, dass die Anzahl der Personen mit einem IQ über dem Durchschnitt gleich der Anzahl der Personen mit einem IQ unter dem Durchschnitt ist. Die Glockenform der Kurve verdeutlicht dies.
Die IQ-Skala ist so konzipiert, dass sie der Gaußschen Normalverteilung entspricht. Die Standardabweichung, ein Maß für die Streuung in der Gruppe, beträgt 15 Punkte. Deshalb liegt ein IQ von 115 eine Standardabweichung über dem Durchschnitt und ein IQ von 70 zwei Standardabweichungen unter dem Durchschnitt.
B197 Führerschein: Alles, Was Du Wissen Musst
Es ist wichtig zu beachten, dass die Gaußsche Normalverteilung eine Idealisierung ist. In der Realität können IQ-Scores leicht von dieser Verteilung abweichen.
Trotz ihrer begrenzten Genauigkeit ist die Gaußsche Normalverteilung ein nützliches Werkzeug zur Quantifizierung der Intelligenz. Sie ermöglicht es uns, die Leistung eines Individuums relativ zur allgemeinen Bevölkerung zu messen.
Abschließend lässt sich sagen, dass das Verständnis der Gaußschen Normalverteilung und ihrer Anwendung auf IQ-Werte für das Verständnis von Intelligenztrends von entscheidender Bedeutung ist. Sie liefert wertvolle Einblicke in die Verteilung der Intelligenz in verschiedenen Populationen und ermöglicht es uns, die Intelligenz auf einer standardisierten Skala zu messen und zu vergleichen.
Logarithmische Normalverteilung
Die logarithmische Normalverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie tritt auf, wenn der natürliche Logarithmus einer Variablen normalverteilt ist. Das bedeutet, dass, wenn eine Zufallsvariable X lognormal verteilt ist, dann ist die Zufallsvariable Y = ln(X) normal verteilt.
Verschiedene Naturschauspiele folgen dieser Verteilung. Beispiele sind bestimmte Speziespopulationen und die Größenverteilung von Partikeln. Sie wird auch in verschiedenen Bereichen der Wissenschaft und Technik verwendet, beispielsweise in der Hydrologie und der Finanzmathematik.
Die Verteilung ist definiert durch zwei Parameter: den Mittelwert (µ) und die Standardabweichung (σ) des natürlichen Logarithmus der Zufallsvariablen. Der Erwartungswert und die Varianz der Lognormalverteilung können in Bezug auf diese Parameter ausgedrückt werden.
Die Form der lognormalen Verteilung ändert sich je nach Wert von µ und σ. Für µ = 0 und σ = 1 erhalten wir die Standardlognormalverteilung. Dies ist eine schiefe Verteilung, die nach rechts ausläuft und ihren Modus bei 1 hat.
Die Wahrscheinlichkeitsdichtefunktion (pdf) einer lognormalen Verteilung ist eine Glockenkurve, die jedoch aufgrund der logarithmischen Transformation nach rechts verschoben und verzerrt ist. Die Fläche unter der Kurve entspricht 1, was die Gesamtwahrscheinlichkeit darstellt.
Stundenzettel Vorlage: Effiziente Zeiterfassung Leicht Gemacht
Die kumulative Verteilungsfunktion (cdf) einer lognormalen Verteilung gibt die Wahrscheinlichkeit an, dass eine Zufallsvariable X einen Wert kleiner oder gleich x annimmt. Sie ist eine stetig ansteigende Funktion von 0 bis 1.
Die logarithmische Normalverteilung hat mehrere nützliche Eigenschaften. Sie ist immer positiv, was sie für Variablen geeignet macht, die nicht negativ sein können, wie beispielsweise Preise oder Populationen. Darüber hinaus bleibt das Produkt von lognormal verteilten Variablen ebenfalls lognormal verteilt.
Obwohl die logarithmische Normalverteilung in vielen Bereichen weit verbreitet ist, hat sie auch ihre Nachteile. Insbesondere kann sie nicht verwendet werden, wenn negative Werte möglich sind, und sie kann übermäßig empfindlich auf extreme Werte reagieren.
Test Auf Normalverteilung Excel
Eine Test auf Normalverteilung in Excel ist eine statistische Methode, die überprüft, ob die Daten in Ihrer Excel-Tabelle einer Normalverteilung folgen oder nicht. Diese Überprüfung ist besonders wichtig, da viele statistische Tests und Modelle auf der Annahme basieren, dass die Daten normalverteilt sind.
Zum Testen auf Normalverteilung in Excel können Sie verschiedene Methoden verwenden. Eine gängige Methode ist der Shapiro-Wilk-Test, ein leistungsfähiger Test für das Vorliegen einer Normalverteilung. Eine andere Methode ist der Anderson-Darling-Test, der empfindlicher auf Abweichungen in den Schwänzen der Verteilung reagiert.
Zum Durchführen dieser Tests benötigen Sie jedoch spezielle statistische Software oder Add-Ins für Excel, da diese Funktionen in Excel nicht standardmäßig verfügbar sind. Einige dieser Add-Ins sind beispielsweise XLSTAT, NumXL oder Analyse-it.
Eine alternative Methode, die direkt in Excel verfügbar ist, ist der Erzeugung eines Histogramms oder eines Quantil-Quantil-Diagramms (QQ-Diagramms). Diese grafischen Methoden geben Ihnen einen visuellen Eindruck davon, ob Ihre Daten normalverteilt sind oder nicht.
Beste Wahl für Textilreinigung Wäscherei In Hamburg
Ein Histogramm zeigt die Häufigkeitsverteilung Ihrer Daten. Wenn Ihre Daten normalverteilt sind, sollte das Histogramm die Form einer Glockenkurve haben. Abweichungen von dieser Form können auf eine Abweichung von der Normalverteilung hinweisen.
Ein QQ-Diagramm hingegen vergleicht die Quartile Ihrer Daten mit den Quartilen einer Normalverteilung. Wenn die Punkte in diesem Diagramm nahe einer geraden Linie liegen, deutet dies auf eine Normalverteilung hin.
Es ist wichtig zu beachten, dass keine dieser Methoden eine absolute Bestätigung für die Normalverteilung Ihrer Daten liefert. Sie sollten immer mehrere Methoden verwenden und die Ergebnisse im Kontext Ihrer spezifischen Forschungsfrage interpretieren.
Zusammenfassend lässt sich sagen, dass Excel eine nützliche Werkzeugkiste für statistische Analysen bieten kann, insbesondere wenn es um die Überprüfung der Normalverteilung geht. Mit den richtigen Tools und dem nötigen Verständnis für die zugrunde liegenden Konzepte können Sie sicherstellen, dass Ihre Datenanalyse auf soliden Grundlagen basiert.
Excel Normalverteilung Diagramm
Ein Normalverteilungsdiagramm, auch als Glockenkurve bezeichnet, ist ein Diagrammtyp, der eine wahrscheinlichkeitsbasierte Verteilung repräsentiert. Es ist ein effektives Werkzeug in Excel zur Visualisierung und Analyse von datengesteuerten Trends und Mustern.
Die Hauptmerkmale dieser Verteilung sind ihr mittlerer Wert (oder Durchschnitt) und die Standardabweichung. Der Durchschnitt ist der zentrale Punkt der Verteilung, um den herum sich die Daten gruppieren. Die Standardabweichung hingegen gibt die Breite der Verteilung an und zeigt, wie weit die Datenpunkte im Durchschnitt vom Durchschnittswert abweichen.
Wendela Horz – Die Antiquitäten-Expertin
Um ein Normalverteilungsdiagramm in Excel zu erstellen, benötigen Sie zunächst einen Datensatz. Der Datensatz kann aus beliebigen numerischen Werten bestehen, wie z.B. Verkaufsdaten, Testergebnissen oder Messwerten.
Nachdem Sie den Datensatz vorbereitet haben, können Sie das Diagramm erstellen. Zuerst erstellen Sie einen Histogramm-Chart mit Ihren Daten. Dann fügen Sie eine Trendlinie hinzu, die die Normalverteilungskurve repräsentiert. Dies kann durch den Zugriff auf das Menü “Trendlinie hinzufügen” in Excel erreicht werden.
Innerhalb dieses Trendlinienmenüs gibt es die Möglichkeit, die Normalverteilungskurve anzupassen. Sie können die Farbe, Dicke und den Stil der Linie wählen. Sie können auch entscheiden, ob Sie die Gleichung und/oder den R²-Wert auf dem Diagramm anzeigen möchten.
Es ist wichtig zu bedenken, dass, obwohl ein Normalverteilungsdiagramm ein nützliches Werkzeug zur Darstellung der Datenverteilung ist, es nicht immer eine genaue Darstellung der Realität ist. Es ist möglich, dass die Daten nicht normal verteilt sind und das Diagramm daher irreführend sein kann.
Zu guter Letzt, das Wissen, wie man ein Normalverteilungsdiagramm in Excel erstellt, ist eine wertvolle Fähigkeit für jeden, der mit Daten arbeitet. Es ermöglicht eine klare und verständliche Darstellung komplexer Daten, was die Analyse und Interpretation der Daten einfacher macht.
Normalverteilung Binomialverteilung
Die Normalverteilung und die Binomialverteilung sind zwei grundlegende Konzepte in der Statistik. Beide Verteilungen haben spezifische Eigenschaften und Anwendungen, die sie für unterschiedliche statistische Analysen geeignet machen.
Die Normalverteilung, auch als Gauß’sche Verteilung bekannt, ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie wird durch zwei Parameter charakterisiert: den Mittelwert (μ), der die Lage der Verteilung bestimmt, und die Standardabweichung (σ), die die Streuung der Verteilung bestimmt. Eine charakteristische Eigenschaft der Normalverteilung ist ihre Glockenform, die bedeutet, dass die meisten Beobachtungen um den Mittelwert gruppiert sind.
Günstige Parfümalternativen Duftzwillinge Liste
Die Binomialverteilung hingegen ist eine diskrete Wahrscheinlichkeitsverteilung. Sie beschreibt die Anzahl der Erfolge in einer festgelegten Anzahl von gleichartigen und unabhängigen Versuchen. In der Binomialverteilung gibt es zwei Parameter: die Anzahl der Versuche (n) und die Wahrscheinlichkeit des Erfolgs (p) in jedem Versuch.
Die Normalverteilung wird oft verwendet, wenn man eine große Anzahl von unabhängigen und identisch verteilten Zufallsvariablen betrachtet. Zum Beispiel kann sie verwendet werden, um die Verteilung von Messfehlern oder die Verteilung von IQ-Scores in einer Bevölkerung zu modellieren.
Die Binomialverteilung wird in Situationen verwendet, in denen das Ergebnis eines Experiments nur zwei mögliche Ergebnisse hat (Erfolg oder Misserfolg). Zum Beispiel könnte sie verwendet werden, um die Anzahl der Köpfe in einer bestimmten Anzahl von Münzwürfen zu modellieren.
Es gibt einen Zusammenhang zwischen der Binomialverteilung und der Normalverteilung. Wenn die Anzahl der Versuche in einer Binomialverteilung groß genug ist (und die Wahrscheinlichkeit des Erfolgs nicht zu nahe an 0 oder 1 liegt), dann kann die Binomialverteilung durch eine Normalverteilung approximiert werden. Dies wird als Normalapproximation der Binomialverteilung bezeichnet.
Zusammenfassend lässt sich sagen, dass sowohl die Normalverteilung als auch die Binomialverteilung grundlegende Werkzeuge in der Statistik sind, die es uns ermöglichen, die Welt um uns herum besser zu verstehen und Vorhersagen über zukünftige Ereignisse zu treffen. Jede Verteilung hat ihre spezifischen Anwendungsfälle und ist wertvoll innerhalb ihres eigenen Kontexts.
Test Normalverteilung
Die Normalverteilung, auch bekannt als Gaußsche Verteilung, ist eine der am häufigsten verwendeten Wahrscheinlichkeitsverteilungen in den Natur- und Sozialwissenschaften. Sie wird durch ihre Glockenkurvenform charakterisiert, die durch den Mittelwert und die Standardabweichung bestimmt wird.
Ein Leitfaden Zum Von Trüffel Kaufen
Der Mittelwert, auch Durchschnittswert genannt, ist der Wert, um den die Datenpunkte zentriert sind. Er ist der Erwartungswert der Normalverteilung. Die Standardabweichung hingegen ist ein Maß für die Streuung der Daten um den Durchschnittswert. Eine kleine Standardabweichung bedeutet, dass die Daten näher am Durchschnitt liegen, während eine große Standardabweichung eine breitere Verteilung der Daten anzeigt.
Eine weitere wichtige Eigenschaft der Normalverteilung ist die Symmetrie. Das bedeutet, dass die Hälfte der Datenpunkte über dem Mittelwert und die andere Hälfte unter dem Mittelwert liegt. Dies ist besonders nützlich für statistische Analysen, da es eine einfache Berechnung von Konfidenzintervallen und Hypothesentests ermöglicht.
Die Normalverteilung hat auch eine bedeutsame Beziehung zu anderen statistischen Konzepten, wie dem zentralen Grenzwertsatz. Dieser Satz besagt, dass die Summe einer großen Anzahl von unabhängigen und identisch verteilten Zufallsvariablen unabhängig von ihrer spezifischen Verteilung eine annähernd normalverteilte Verteilung hat.
Da die Normalverteilung eine kontinuierliche Verteilung ist, können wir sie nicht direkt in Tabellenform darstellen. Stattdessen verwenden wir die Normalverteilungsfunktion, um die Wahrscheinlichkeit zu berechnen, dass eine Zufallsvariable einen bestimmten Wert oder weniger annimmt.
Es ist auch wichtig zu beachten, dass nicht alle Daten normalverteilt sind. In der Praxis gibt es viele Beispiele für Daten, die nicht normalverteilt sind. In diesen Fällen können andere statistische Methoden und Verteilungen besser geeignet sein.
Zusammenfassend lässt sich sagen, dass die Normalverteilung ein mächtiges Werkzeug in der statistischen Analyse ist. Trotz ihrer Einschränkungen bietet sie einen guten Ausgangspunkt für die Modellierung und Analyse von Daten in vielen verschiedenen Bereichen.
Spss Test Auf Normalverteilung
Der SPSS-Test auf Normalverteilung ist ein statistisches Verfahren, das verwendet wird, um zu überprüfen, ob eine Datenmenge normal verteilt ist. Dies ist wichtig, weil viele statistische Tests davon ausgehen, dass die Daten normal verteilt sind.
Die verschiedenen Arten von Feuerzeug
Es gibt mehrere Methoden, um die Normalverteilung in SPSS zu testen. Eine gängige Methode ist der Kolmogorov-Smirnov-Test, der die empirische Verteilungsfunktion einer Stichprobe mit der Verteilungsfunktion einer Referenzverteilung vergleicht.
Eine andere Methode ist der Shapiro-Wilk-Test. Dieser Test ist besonders nützlich für kleine Stichprobengrößen. Er vergleicht die Reihenfolge der Werte in der Stichprobe mit der Reihenfolge, die von einer Normalverteilung erwartet wird.
Darüber hinaus kann die Normalverteilung auch visuell mit einem Histogramm oder einem Quantil-Quantil-Plot beurteilt werden. Ein Histogramm zeigt die Verteilung der Daten, während ein Q-Q-Plot die Daten gegen eine theoretische Normalverteilung aufträgt.
Es ist wichtig zu beachten, dass kein Test die Normalverteilung mit absoluter Sicherheit bestätigen kann. Stattdessen liefern sie Beweise, die die Annahme der Normalverteilung unterstützen oder widerlegen können.
Wenn die Daten nicht normal verteilt sind, gibt es verschiedene Möglichkeiten, damit umzugehen. Eine Möglichkeit besteht darin, eine Transformation durchzuführen, wie zum Beispiel eine logistische oder eine Box-Cox-Transformation.
Eine andere Möglichkeit besteht darin, nicht-parametrische Methoden zu verwenden, die keine Voraussetzungen für die Verteilung der Daten machen. Diese Methoden sind oft leistungsfähiger als ihre parametrischen Gegenstücke, wenn die Annahmen der Normalverteilung verletzt sind.
Zusammenfassend kann gesagt werden, dass der SPSS-Test auf Normalverteilung ein wichtiges Werkzeug in der statistischen Analyse ist. Er hilft den Forschern zu verstehen, ob ihre Daten normal verteilt sind und welche Analysemethoden daher am geeignetsten sind.
Normalverteilung Intelligenz
Die Normalverteilung ist eine Schlüsselkonzeption in der Statistik und wird oft zur Darstellung realer Phänomene verwendet, einschließlich der Intelligenz. In der Psychologie ist die Intelligenz normalverteilt, was bedeutet, dass die meisten Menschen eine durchschnittliche Intelligenz haben, während weniger Menschen sehr hohe oder sehr niedrige Intelligenzwerte aufweisen.
Balkonkraftwerk mit Speicher – Nachhaltige Energiequelle
Die Glockenkurve ist eine visuelle Darstellung der Normalverteilung. Im Kontext der Intelligenzverteilung stellt die Mitte der Glockenkurve den durchschnittlichen Intelligenzquotienten (IQ) dar, der üblicherweise auf 100 festgelegt ist. Die Kurve ist symmetrisch, was bedeutet, dass die Anzahl der Personen mit einem IQ über dem Durchschnitt gleich der Anzahl der Personen mit einem IQ unter dem Durchschnitt ist.
In der Psychometrie wird die Standardabweichung häufig zur Messung der Streuung in einer normalverteilten Stichprobe verwendet. Eine Standardabweichung ist der durchschnittliche Abstand zwischen jedem Datenpunkt und dem Durchschnitt. In Bezug auf den IQ ist eine Standardabweichung von 15 üblich, was bedeutet, dass die meisten Menschen (etwa 68%) einen IQ zwischen 85 und 115 haben.
Wenn wir weiter von der Mitte der Glockenkurve weggehen, nimmt die Anzahl der Menschen mit diesem IQ ab. Etwa 95% der Bevölkerung haben einen IQ zwischen 70 und 130, was zwei Standardabweichungen vom Durchschnitt entspricht. Nur 2,5% der Menschen haben einen IQ unter 70 oder über 130.
Es ist wichtig zu beachten, dass die normale Verteilung der Intelligenz basierend auf der Definition von „normal“ in der Statistik ist. Es bedeutet nicht, dass Menschen mit einem IQ außerhalb des Durchschnittsbereichs “abnormal” sind. Vielmehr gibt es in jeder Bevölkerung eine natürliche Variation in Bezug auf viele Merkmale, einschließlich der Intelligenz.
Die Normalverteilung der Intelligenz hat Auswirkungen auf den Bildungssektor, die Arbeitswelt und viele andere Bereiche des Lebens. Es hilft Bildungsexperten, Lehrpläne und Lehrstrategien zu entwerfen, die auf der Mehrheit der Schüler abgestimmt sind, und Arbeitgebern, potenzielle Mitarbeiter zu bewerten.
Abschließend ist es wichtig zu bedenken, dass, obwohl die Intelligenz normalverteilt ist, sie nicht das einzige Merkmal ist, das den Erfolg oder das Potenzial einer Person bestimmt. Fähigkeiten, Talente, Persönlichkeitsmerkmale und andere Faktoren spielen ebenfalls eine wichtige Rolle.
Standardisierte Normalverteilung
Die standardisierte Normalverteilung, auch Z-Verteilung genannt, ist eine spezielle Form der Normalverteilung. Sie hat einen Erwartungswert von null und eine Standardabweichung von eins. Diese speziellen Eigenschaften machen sie in vielen statistischen Anwendungen äußerst nützlich.
Autoschlüssel Nachmachen: Kosten, Anbieter Und Standorte
In der Praxis wird die standardisierte Normalverteilung häufig verwendet, um rohe Daten zu standardisieren. Durch diesen Prozess werden die Datenmengen so transformiert, dass sie unabhängig von ihrer ursprünglichen Verteilung verglichen werden können.
Die Standardisierung wird durch Abzug des Erwartungswertes und anschließende Division durch die Standardabweichung erreicht. Das Ergebnis ist eine Verteilung mit einem Mittelwert von null und einer Standardabweichung von eins. Dies ermöglicht es, die Position eines Datenpunkts innerhalb der Verteilung zu bestimmen.
Die Fläche unter der Kurve der standardisierten Normalverteilung entspricht 1. Dies bedeutet, dass die Wahrscheinlichkeit, dass ein zufällig ausgewählter Wert innerhalb der Verteilung liegt, 100% beträgt.
Die standardisierte Normalverteilung wird auch in vielen statistischen Tests verwendet, wie dem t-Test und dem Chi-Quadrat-Test. In diesen Tests wird die Abweichung einer Stichprobe von der erwarteten Normalverteilung gemessen.
Zusätzlich zur Anwendung in der Statistik wird die standardisierte Normalverteilung auch in anderen Bereichen wie der Quantenphysik und der Finanzmathematik verwendet. In diesen Bereichen liefert die Normalverteilung nützliche Modelle für eine Vielzahl von Phänomenen.
Trotz ihrer Vielseitigkeit hat die standardisierte Normalverteilung auch ihre Grenzen. Sie ist nicht geeignet für Daten, die eine starke Schiefe oder Wölbung aufweisen. In solchen Fällen ist es oft besser, andere statistische Modelle zu verwenden.
Zusammenfassend lässt sich sagen, dass die standardisierte Normalverteilung ein äußerst nützliches Werkzeug in der Statistik und darüber hinaus ist. Ihre Verwendung ermöglicht es uns, komplizierte datengesteuerte Probleme zu lösen und fundierte Entscheidungen zu treffen.
Eine Umfassende Zum Islandpferd Kaufen
Zusammenfassung
Die Normalverteilung ist eine zentrale Konzept in der Statistik und findet breite Anwendung in verschiedenen Bereichen. Sie wird durch ihren Mittelwert und ihre Standardabweichung charakterisiert. Obwohl nicht alle Daten normalverteilt sind, dient die Normalverteilung als wichtiges Werkzeug für statistische Analysen und Modellierungen. Die Kenntnis über die Normalverteilung und ihre Eigenschaften ist für jeden, der mit Daten arbeitet, von großer Bedeutung.
Besuchen Sie für weitere erstaunliche Updates weiterhin Nachrichten Morgen.