Ein Koordinatensystem ist ein grundlegendes Werkzeug in der Mathematik und anderen Wissenschaften, das es ermöglicht, Punkte und Positionen in einem Raum zu beschreiben und zu veranschaulichen. Es besteht aus einer Reihe von Achsen und Quadranten, die es uns ermöglichen, verschiedene Punkte oder Positionen eindeutig zu definieren.
In diesem Blog werden wir uns mit den verschiedenen Aspekten eines Koordinatensystems befassen und die Bedeutung der häufig verwendeten Begriffe klären. Von den Grundlagen bis zu komplexeren 3D-Koordinatensystemen werden wir alles behandeln.
Was ist ein Koordinatensystem?
Ein Koordinatensystem ist ein mathematisches System, das aus zwei oder mehr Achsen besteht. Diese Achsen sind senkrecht zueinander angeordnet und treffen sich in einem Punkt, der als Ursprung bezeichnet wird. Punkte in diesem System werden durch eine Reihe von Zahlen oder Koordinaten dargestellt, die entlang der Achsen gemessen werden.
Stundenzettel Vorlage: Effiziente Zeiterfassung Leicht Gemacht
Das kartesische Koordinatensystem:
Das kartesische Koordinatensystem ist das bekannteste und am häufigsten verwendete Koordinatensystem. Es besteht aus zwei Achsen, der x-Achse (horizontal) und der y-Achse (vertikal), die sich im Ursprung schneiden. Es wird auch als zweidimensionales Koordinatensystem bezeichnet.
Das dreidimensionale Koordinatensystem:
Im dreidimensionalen Koordinatensystem gibt es eine zusätzliche Achse, die z-Achse, die senkrecht zur x- und y-Achse steht. Dies ermöglicht die Darstellung von Punkten im dreidimensionalen Raum. Es wird oft verwendet, um Positionen in der Physik, Ingenieurwissenschaften, Computergrafik und vielen anderen Bereichen darzustellen.
3D-Koordinatensystem online:
Heutzutage gibt es zahlreiche Online-Tools und Software, die es ermöglichen, ein 3D-Koordinatensystem virtuell zu erstellen und damit zu arbeiten. Diese Tools sind besonders nützlich, wenn komplexe 3D-Darstellungen benötigt werden, beispielsweise in der 3D-Modellierung oder in der Geometrie.
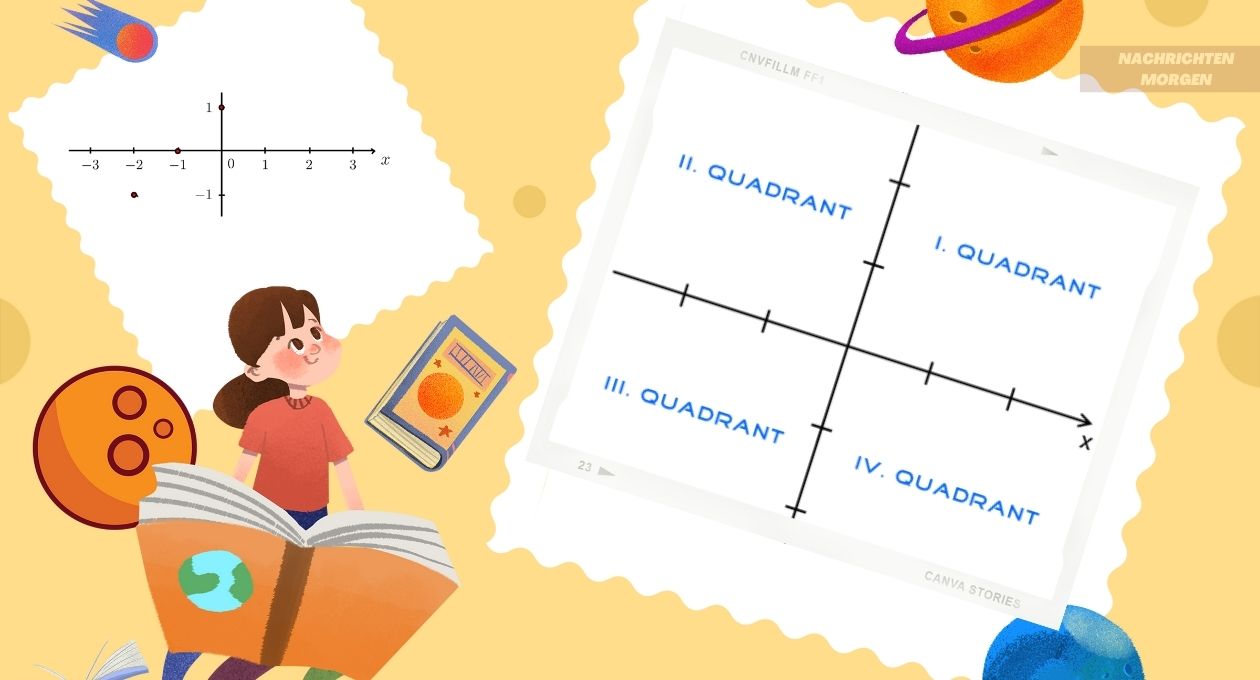
Koordinatensystem Quadranten:
Das kartesische Koordinatensystem ist in vier Quadranten unterteilt, die durch die positiven und negativen Vorzeichen der x- und y-Koordinaten bestimmt werden. Der erste Quadrant liegt in der oberen rechten Ecke und geht im Uhrzeigersinn weiter. Jeder Quadrant hat eine eindeutige Kombination von positiven und negativen Koordinaten.
Quadrant im Koordinatensystem:
Die Quadranten im Koordinatensystem sind in vier Abschnitte unterteilt, die durch die positiven und negativen Werte der x- und y-Koordinaten bestimmt werden. Der erste Quadrant befindet sich bei einem kartesischen Standardkoordinatensystem in der oberen rechten Ecke. Dieser Quadrant hat sowohl positive als auch negative x- und y-Werte, die als (+x, +y) bezeichnet werden.
Der zweite Quadrant befindet sich in der oberen linken Ecke und hat negative x-Werte, aber positive y-Werte, bezeichnet als (-x, +y). Der dritte Quadrant befindet sich in der unteren linken Ecke und hat negative x-Werte und negative y-Werte, bezeichnet als (-x, -y). Der vierte Quadrant schließlich befindet sich in der rechten unteren Ecke mit positiven x-Werten und negativen y-Werten, bezeichnet als (+x, -y).
Jeder dieser vier Bereiche kann weiter in acht Oktanten unterteilt werden. Oktanten bezeichnen 45°-Winkel zwischen zwei beliebigen Achsen. Wenn wir zum Beispiel jeden unserer vier Abschnitte in zwei 45°-Winkel entlang beider Achsen unterteilen, haben wir alle acht Oktanten. Jede Oktante hat ihre eigene Kombination von Vorzeichen für jede Achse und ihre jeweiligen Werte.
Quadranten und Oktanten spielen in der Mathematik eine wichtige Rolle, da sie zur Beschreibung von Positionen im Raum verwendet werden, wenn Punkte in einem Diagramm oder einer Ebene aufgetragen werden. Außerdem können sie beim Lösen von Gleichungen mit drei oder mehr Variablen nützlich sein. Wenn man weiß, wie man sie richtig einsetzt, kann das Lösen von Problemen viel einfacher sein.
Jeder Quadrant im Koordinatensystem hat seine eigene Besonderheit. Im ersten Quadranten sind beide Koordinaten positiv, im zweiten ist die x-Koordinate negativ, im dritten sind beide negativ und im vierten ist die y-Koordinate negativ. Die Kenntnis der Quadranten ist wichtig, um Winkel und Richtungen korrekt zu berechnen.
Koordinatensystem XYZ
Das XYZ-Koordinatensystem ist eine andere Bezeichnung für das dreidimensionale Koordinatensystem, wobei X, Y und Z die Bezeichnungen der Achsen sind. Es wird häufig in der Mathematik, Physik und 3D-Grafik verwendet.
Koordinatensystem X, Y, Z
Das XYZ-Koordinatensystem ist ein dreidimensionales Koordinatensystem, das in der Mathematik, Physik und 3D-Grafik verwendet wird. Es besteht aus drei Achsen: X, Y und Z. Die X-Achse verläuft horizontal von links nach rechts, die Y-Achse vertikal von unten nach oben und die Z-Achse in der Tiefe von vorne nach hinten. Jede Position im Raum kann durch eine eindeutige Kombination von Koordinaten auf jeder Achse identifiziert werden. Ein Punkt, der sich beispielsweise fünf Einheiten entlang der X-Achse, sieben Einheiten entlang der Y-Achse und zwei Einheiten entlang der Z-Achse befindet, hätte die XYZ-Koordinate (5, 7, 2).
In diesem System hat jeder Punkt im Raum auf jeder Achse einen positiven oder negativen Wert. Wenn alle Werte positiv oder Null sind, liegt dieser Punkt im so genannten ersten Oktanten des Raums – oder allgemeiner ausgedrückt, im ersten Quadranten für jede einzelne Achse. Wenn einer der Werte negativ ist, liegt er in einem der anderen sieben Oktanten (Quadranten) des Raums. Diese anderen Oktanten (Quadranten) können als Spiegelungen oder Drehungen des ersten Oktanten um seinen Ursprung betrachtet werden.
B197 Führerschein: Alles, Was Du Wissen Musst
Dies ermöglicht die Berechnung von Winkeln und Richtungen in Bezug auf diese Achsen. Wenn zum Beispiel zwei Punkte durch ein Liniensegment verbunden sind, hat dieses Liniensegment einen Winkel zwischen ihm und einer oder mehreren Achsen, je nach seiner Ausrichtung relativ zu ihnen. Wenn man weiß, in welchem Quadranten es sich befindet, lässt sich dieser Winkel leichter bestimmen, als wenn man nur die Koordinaten eines Punktes kennt.
Das XYZ-Koordinatensystem ist besonders nützlich für die Darstellung von Objekten in der 3D-Computergrafik, weil es uns erlaubt, ihre genaue Position und Ausrichtung im Raum mit einfachen Zahlen zu definieren. Dies macht es nicht nur für Computer, sondern auch für Menschen einfach zu verstehen, wie sich Objekte in einer virtuellen 3D-Umgebung räumlich zueinander verhalten.
Ähnlich wie oben beschrieben, bezieht sich das Koordinatensystem X, Y, Z auf ein dreidimensionales System mit den Achsen X, Y und Z. Es ermöglicht die eindeutige Positionierung von Punkten im dreidimensionalen Raum.
Koordinatensystem XY
Das Koordinatensystem XY ist eine andere Bezeichnung für das zweidimensionale Koordinatensystem. Es besteht aus den Achsen X und Y, die senkrecht zueinander stehen und den Punkt (0,0) als Ursprung haben.
Koordinatensystem XY – Was zuerst
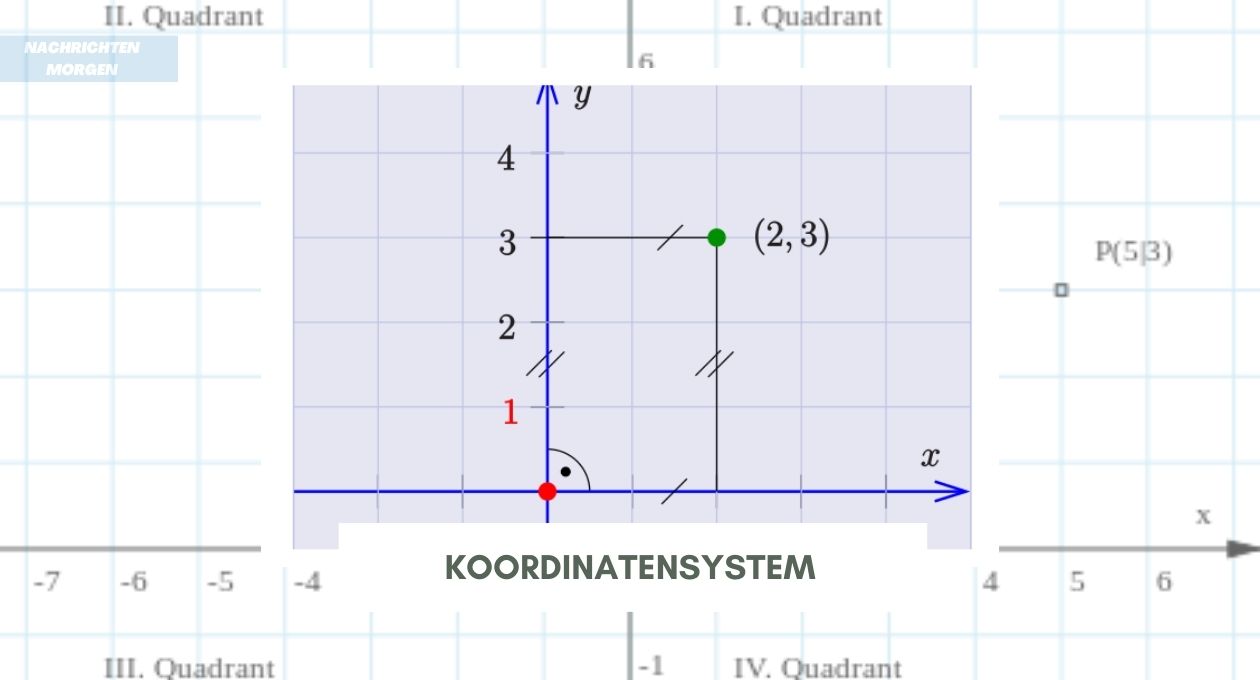
Das XY-Koordinatensystem ist ein zweidimensionales Koordinatensystem, mit dem man Punkte in einer Ebene lokalisieren kann. Dieses System besteht aus zwei Achsen, der X-Achse und der Y-Achse, die sich im Ursprung (0, 0) kreuzen. Die X-Achse verläuft im Allgemeinen horizontal durch die Ebene, während die Y-Achse vertikal verläuft. Durch die Lokalisierung von Punkten auf diesen beiden Achsen können wir die Koordinaten eines beliebigen Punktes im zweidimensionalen Raum bestimmen. Befindet sich zum Beispiel ein Punkt bei (3, 4), dann wären seine Koordinaten drei Einheiten entlang der X-Achse und vier Einheiten entlang der Y-Achse.
Im Koordinatensystem werden zuerst die X-Koordinate und dann die Y-Koordinate angegeben. Wenn wir zum Beispiel den Punkt (3, 4) haben, bedeutet dies, dass wir zuerst entlang der X-Achse 3 Einheiten nach rechts und dann entlang der Y-Achse 4 Einheiten nach oben gehen.
Was ist ein Vektor-Koordinatensystem?
Ein Vektor-Koordinatensystem ist eine Erweiterung des normalen Koordinatensystems, bei dem jedem Punkt nicht nur eine Position, sondern auch ein Vektor zugeordnet ist. Vektoren haben sowohl eine Richtung als auch eine Länge und werden oft verwendet, um physikalische Größen wie Geschwindigkeit, Beschleunigung oder Kraft darzustellen.
Vektoren im Koordinatensystem
Die Darstellung von Vektoren im Koordinatensystem erfolgt durch Pfeile, die vom Ursprung zu einem bestimmten Punkt zeigen. Der Pfeil zeigt die Richtung des Vektors an, und seine Länge gibt die Größe oder den Betrag des Vektors an.
Koordinatensystem erstellen.
Um ein Koordinatensystem zu erstellen, benötigt man lediglich zwei (für 2D) oder drei (für 3D) senkrecht zueinander stehende Linien, die sich im Ursprung schneiden. Die Linien werden als Achsen bezeichnet und bilden die Grundlage für die Darstellung von Punkten im Raum.
Stundenplan: Eine praktische Anleitung zum Erstellen und Verwalten
Koordinatensystem punkte eintragen
Ein Punkt in einem Koordinatensystem ist ein Ort im Raum, der durch die Koordinaten seiner Position entlang jeder Achse identifiziert wird. Zum Beispiel hat der Punkt (3, 4) die x-Koordinate 3 und die y-Koordinate 4. In einem 3D-Koordinatensystem kann ein Punkt auch drei Koordinaten haben, die seine Position entlang der x-, y- und z-Achse angeben. Punkte können verwendet werden, um physische Objekte wie Gebäude oder Orte auf einer Karte darzustellen.
Sie können auch verwendet werden, um Funktionen oder Gleichungen in mehreren Dimensionen darzustellen. Es ist wichtig, daran zu denken, dass alle Punkte eindeutige Koordinaten haben müssen, damit sie innerhalb des Koordinatensystems genau lokalisiert werden können.
Das Eintragen von Punkten in ein Koordinatensystem ist eine grundlegende Aufgabe. Dabei werden die Koordinaten des Punktes entlang der entsprechenden Achsen abgelesen und eingetragen.
Koordinatensystem leer
Ein leeres Koordinatensystem ist ein unbeschriftetes oder unmarkiertes Koordinatensystem, das noch keine Punkte oder Linien enthält. Es ist eine leere Vorlage, die für verschiedene Zwecke verwendet werden kann, wie z. B. für mathematische Übungen oder grafische Darstellungen.
Koordinatensystem PDF
Ein Koordinatensystem im PDF-Format kann als Vorlage zum Ausdrucken verwendet werden. Es ist praktisch, um eine leere Vorlage zu haben, auf der man Punkte eintragen oder grafische Darstellungen vornehmen kann.
Vorlage Koordinatensystem
Eine Vorlage für ein Koordinatensystem ist ein vordefiniertes leeres Koordinatensystem, das als Grundlage für verschiedene Zeichnungen oder Aufgaben dienen kann. Es spart Zeit und ist besonders nützlich für Lehrer, Schüler und Ingenieure.
Koordinatensystem zeichnen
Das Zeichnen eines Koordinatensystems ist einfach und erfordert nur die Platzierung der Achsen und das Hinzufügen der Beschriftungen für die Achsen. Danach können Punkte oder Kurven gezeichnet werden, um verschiedene Informationen zu veranschaulichen.
UTM-Koordinatensystem
Das UTM-Koordinatensystem (Universal Transverse Mercator) ist ein globales Koordinatensystem, das verwendet wird, um Punkte auf der Erdoberfläche zu lokalisieren. Es basiert auf einem transversalen Mercator-Projektionsverfahren und teilt die Welt in 6-Grad-Breitengradzonen ein.
Glückwünsche Zum 60. Geburtstag: Eine Sammlung Von Grüßen
Koordinatensystem Mathe
Das Koordinatensystem ist ein wesentlicher Bestandteil der Mathematik und wird verwendet, um eine Vielzahl von Konzepten und Problemen zu visualisieren und zu lösen. Es ist die Grundlage für die Analyse von Funktionen, Geometrie, Trigonometrie und vielen weiteren mathematischen Disziplinen.
Mathe Koordinatensystem
Das mathematische Koordinatensystem ist ein wichtiges Hilfsmittel in der Mathematik, das es uns ermöglicht, komplexe mathematische Probleme zu visualisieren und zu lösen. Es wird verwendet, um Punkte, Linien, Kurven und andere Objekte im zwei- oder dreidimensionalen Raum darzustellen. Mithilfe des Koordinatensystems können Mathematiker Punkte in ein Diagramm einzeichnen oder eine Kurve abbilden, um die Lösung von Gleichungen zu finden.
Im zweidimensionalen Koordinatensystem werden Punkte durch ihre x-Koordinaten (horizontale Achse) und y-Koordinaten (vertikale Achse) beschrieben. Der Punkt (x, y) liegt dann im Schnittpunkt dieser Achsen. Im dreidimensionalen Raum werden die Punkte durch ihre x-, y- und z-Koordinaten beschrieben, die ein xyz-Koordinatensystem bilden.
Der Ursprung ist der Punkt, von dem alle Koordinaten ausgehen, und wird gewöhnlich mit (0, 0) bezeichnet. Dieser Punkt wird dann als Bezugspunkt für die Darstellung anderer Punkte verwendet, die je nach ihrer Lage zum Ursprung positive oder negative Werte entlang jeder Achse haben. Wenn wir zum Beispiel einen Punkt (4, 5) haben, bedeutet dies, dass er 4 Einheiten entlang der x-Achse und 5 Einheiten entlang der y-Achse vom Ursprung entfernt liegt.
Das kartesische Koordinatensystem ist eine Art von mathematischem Koordinatensystem, das reelle Zahlen für seine Koordinaten verwendet. Andere Arten von mathematischen Koordinatensystemen sind Polarkoordinaten, die Winkel und Abstände von einem festen Ursprung verwenden; Kugelkoordinaten, die Winkel zwischen drei Ebenen verwenden; Zylinderkoordinaten, die Abstände in drei Richtungen verwenden; und Ellipsoidkoordinaten, die Abstände zwischen zwei Brennpunkten messen.
Koordinatensysteme bieten eine effektive Möglichkeit, Datensätze in der Mathematik zu organisieren, so dass Probleme mit größerer Genauigkeit gelöst werden können. Auch in der Physik und im Ingenieurwesen werden sie häufig verwendet, um physikalische Objekte wie Planeten zu modellieren oder die auf sie wirkenden Kräfte zu analysieren.
Das Koordinatensystem in der Mathematik ist ein visuelles Hilfsmittel, um mathematische Konzepte zu veranschaulichen und zu analysieren. Es ermöglicht die graphische Darstellung von Funktionen, die Lösung geometrischer Probleme und die Berechnung von Koordinaten.
Koordinatensystem Punkte
Punkte im Koordinatensystem werden durch ihre Koordinaten repräsentiert. Ein Punkt im zweidimensionalen Koordinatensystem hat zwei Koordinaten (x, y), während ein Punkt im dreidimensionalen Koordinatensystem drei Koordinaten (x, y, z) hat.
Koordinatensystem eintragen
Das Eintragen von Punkten in ein Koordinatensystem bedeutet, die Koordinaten des Punktes entlang der entsprechenden Achsen einzutragen. Dadurch wird die Position des Punktes im Raum festgelegt.
Koordinatensystem übungen
Übungen zum Koordinatensystem sind eine gute Möglichkeit, das Verständnis der grundlegenden Konzepte zu vertiefen. Es kann Aufgaben wie das Eintragen von Punkten, das Zeichnen von Kurven oder das Lösen geometrischer Probleme umfassen.
Warum Darf Man Sterbende Nicht Beim Namen Rufen?
Räumliches Koordinatensystem
Problem: Das Verständnis und die Analyse mathematischer Konzepte kann schwierig sein, insbesondere wenn es um räumliche Koordinatensysteme geht.
Rühren: Der Versuch, die verschiedenen Koordinaten und Achsen eines Koordinatensystems zu verstehen, kann für SchülerInnen überwältigend sein und zu Verwirrung und Frustration führen.
Lösung: Mit den richtigen Übungen wird das Verständnis räumlicher Koordinatensysteme einfacher. Durch das Einzeichnen von Punkten, das Zeichnen von Kurven und das Lösen geometrischer Probleme mit einem Koordinatensystem können Sie schnell ein intuitives Verständnis für die Funktionsweise dieser Systeme entwickeln. Dies wird Ihnen helfen, mathematische Konzepte in Zukunft besser zu analysieren..
Das räumliche Koordinatensystem ist ein Synonym für das dreidimensionale Koordinatensystem. Es wird verwendet, um Punkte im dreidimensionalen Raum zu lokalisieren und zu beschreiben.
Graphen im Koordinatensystem
Graphen sind visuelle Darstellungen von Funktionen oder Daten im Koordinatensystem. Sie bestehen aus Linien, Kurven oder anderen geometrischen Formen, die die Beziehung zwischen den Variablen darstellen.
Funktionale Abhängigkeit im Koordinatensystem
Die funktionale Abhängigkeit im Koordinatensystem beschreibt, wie sich die Position eines einzelnen Punktes oder eines ganzen Diagramms in Abhängigkeit von einer oder mehreren unabhängigen Variablen verändert. Dies wird als parametrische Gleichung bezeichnet und kann durch lineare Gleichungen, polynomische Gleichungen, trigonometrische Funktionen oder Exponentialfunktionen ausgedrückt werden.
Wenn wir die funktionale Abhängigkeit im räumlichen Koordinatensystem verstehen, können wir Punkte in einem Diagramm genau darstellen und Beziehungen zwischen Variablen leichter visualisieren. Außerdem können diese Beziehungen dann zur Berechnung von Ableitungen und Integralen für fortgeschrittene mathematische Berechnungen verwendet werden.
Im Koordinatensystem zeigt eine funktionale Abhängigkeit die Beziehung zwischen zwei Variablen an. Eine Variable hängt von der anderen ab und kann daher durch eine mathematische Funktion ausgedrückt werden.
Koordinatensystem zum Ausdrucken
Ein Koordinatensystem zum Ausdrucken ist eine Vorlage im PDF- oder Bildformat, die gedruckt und als leere Arbeitsfläche verwendet werden kann. Es ist eine bequeme Möglichkeit, mathematische Aufgaben oder Zeichnungen ohne den Bedarf an Computer- oder Softwareverwendung durchzuführen.
Winkelhalbierende im Koordinatensystem.
Eine Winkelhalbierende ist eine Linie, die einen Winkel in zwei gleich große Winkel teilt. Im Koordinatensystem kann eine Winkelhalbierende zum Beispiel dazu verwendet werden, den Schnittpunkt zweier Geraden zu finden.
Eine umfassende Liste von Ideen und Antworten Land mit
Koordinatensystem PNG
Ein Koordinatensystem PNG ist ein Bilddateiformat, das zur Erstellung von Bildern und anderen Grafiken verwendet wird. Dieser Dateityp wird häufig in Verbindung mit einem Koordinatensystem verwendet, da er leicht manipuliert werden kann, um die Position und den Winkel von Punkten innerhalb des Systems zu ändern. PNG-Dateien mit Koordinatensystem werden häufig zur Erstellung von visuellen Diagrammen, Tabellen, Zeichnungen und anderen Grafiken verwendet.
Der Vorteil dieses Dateiformats besteht darin, dass es im Vergleich zu anderen Formaten wie JPG oder GIF eine größere Kontrolle über die Platzierung von Punkten in einem Koordinatensystem ermöglicht. Außerdem bieten PNGs eine höhere grafische Auflösung als andere Rasterbildformate, wodurch sie sich für den Druck und die Anzeige auf digitalen Bildschirmen eignen.
Ein Koordinatensystem im PNG-Format ist eine Grafikdatei, die ein Koordinatensystem ohne Hintergrund enthält. PNG-Dateien werden häufig für die Darstellung von Bildern und Grafiken im Internet verwendet.
XYZ-Koordinatensystem online
Online-Tools ermöglichen es Benutzern, ein XYZ-Koordinatensystem virtuell zu erstellen und damit zu arbeiten. Diese Tools bieten oft zusätzliche Funktionen wie das Eintragen von Punkten, das Zeichnen von Linien oder das Erstellen von 3D-Modellen.
Figuren im Koordinatensystem
Im Koordinatensystem können verschiedene geometrische Figuren dargestellt werden, wie zum Beispiel Linien, Dreiecke, Quadrate oder Kreise. Diese Darstellungen ermöglichen es, geometrische Eigenschaften und Beziehungen zu analysieren.
Das Koordinatensystem verstehen
Das Verständnis des Koordinatensystems ist von zentraler Bedeutung für die Mathematik und andere Wissenschaften. Es ermöglicht die Darstellung von Daten, das Lösen von Problemen und das Erstellen von Modellen in einer klaren und präzisen Weise.
Online Koordinatensystem
Online-Koordinatensysteme sind interaktive Tools, die es Benutzern ermöglichen, Koordinatensysteme direkt im Webbrowser zu erstellen und zu manipulieren. Sie sind praktisch und leicht zugänglich, um schnell mathematische Konzepte zu visualisieren.
Koordinatensystem erstellen
Die Erstellung eines Koordinatensystems erfordert nur wenige Schritte. Man beginnt mit dem Zeichnen der Achsen und beschriftet sie mit den entsprechenden Skalen. Danach können Punkte oder Graphen eingetragen werden.
Leeres Koordinatensystem
Ein leeres Koordinatensystem ist eine unbeschriftete Vorlage, die zum Zeichnen oder Eintragen von Punkten verwendet werden kann. Es bietet eine klare Arbeitsfläche, um mathematische Konzepte zu erforschen oder grafische Darstellungen zu erstellen.
Einführung in Die Plattform IServ Obs
Koordinatensystem Beispiele
Beispiele für Koordinatensysteme können eine Vielzahl von mathematischen Funktionen, geometrischen Formen oder realen Datensätzen umfassen. Solche Beispiele helfen dabei, das Verständnis der Funktions weise des Koordinatensystems zu vertiefen.
Vektoren im Koordinatensystem
Vektoren können im Koordinatensystem durch Pfeile dargestellt werden, die vom Ursprung zu einem bestimmten Punkt zeigen. Die Länge und Richtung des Pfeils geben die Größe und Richtung des Vektors an.
Funktion in Koordinatensystem einzeichnen
Das Einzeichnen einer Funktion im Koordinatensystem bedeutet, die Punkte zu markieren, die die Funktionsgleichung erfüllen. Diese Punkte können dann verbunden werden, um den Graphen der Funktion zu zeichnen.
Koordinatensystem blanko
Ein blanko Koordinatensystem ist ein leeres Koordinatensystem ohne Achsenbeschriftungen oder Zahlen. Es ist eine leere Vorlage, die zum Zeichnen oder für mathematische Übungen verwendet werden kann.
Eidesstattliche Erklärung: Definition, Bedeutung
Dreidimensionales Koordinatensystem online
Problem: Die Arbeit mit 3D-Koordinatensystemen kann schwierig und zeitaufwändig sein, vor allem, wenn man nicht die richtigen Werkzeuge zur Verfügung hat.
Rühren: Der Versuch, komplexe mathematische Konzepte in drei Dimensionen zu verstehen, ist schon schwierig genug, ohne dass man sich um die Suche nach der richtigen Software oder Hardware kümmern muss.
Die Lösung: XYZ Coordinate System Online macht es jedem leicht, mit 3D-Koordinatensystemen schnell und einfach von jedem Webbrowser aus zu arbeiten. Mit unserem intuitiven Online-Tool können Sie in einem Bruchteil der Zeit Modelle erstellen, Probleme lösen und Daten visualisieren!
Online-Tools ermöglichen es Benutzern, ein dreidimensionales Koordinatensystem direkt im Webbrowser zu erstellen und zu manipulieren. Diese Tools sind besonders nützlich für komplexe 3D-Darstellungen.
Erstellen Sie Beeindruckende Schriftgenerator
Koordinaten in einem 3D-Koordinatensystem beschriften.
Koordinaten in einem dreidimensionalen Koordinatensystem können mit drei Zahlen beschriftet werden, die angeben, wie weit sie sich entlang jeder Achse befinden. Wenn zum Beispiel der Punkt (3, 4, 5) auf einer XYZ-Koordinatenebene eingezeichnet ist, befindet er sich drei Einheiten
Fazit
Das Koordinatensystem ist ein grundlegendes mathematisches Werkzeug, das zur Darstellung von Daten, zur Lösung von Problemen und zur Entdeckung von Beziehungen verwendet wird. Das Verständnis der Grundlagen des Koordinatensystems ist für jeden Mathematiker oder Wissenschaftler unerlässlich.
Die Beispiele in diesem Artikel geben einen guten Überblick über die vielfältigen Einsatzmöglichkeiten des Koordinatensystems. Mit etwas Übung kann man das Erstellen und Manipulieren von Koordinatensystemen sowohl auf Papier als auch online beherrschen.
Besuchen Sie für weitere erstaunliche Updates weiterhin Nachrichten Morgen.